The African Institute for Mathematical Sciences Ghana (AIMS Ghana) is inviting applications for the African Mathematical School (AMS) in “Mathematical Methods in Analysis and Probability (2MAP)”scheduled from August 16 to 27, 2021 at AIMS Ghana in Accra. The school is organized within the framework of the AMU/CIMPA.
Organized around eight (8) courses, and three (3) advanced lectures, the highly interactive 2MAP will bring together renowned international and national scientific researchers and graduate students working on functional analysis, calculus of variations, kinetic theory, partial differential equations, gradient flow theory, stochastic analysis, stochastic differential equations and related numerical methods.
AIMS School Coordinators
– Olivier Menoukeu Pamen: African Institute for Mathematical Sciences (AIMS) Ghana and University of Liverpool
– Franca Hoffmann: California Institute of Technology
Scientific Committee
– José A. Cañizo, Universidad de Granada, Spain
– Kwabena Doku-Amponsah, University of Ghana
– Emmanuel Essel, University of Cape Coast, Ghana
– Peter Imkeller, Humboldt University Berlin, Germany
– Diaraf Seck, Université Cheikh Anta Diop, Senegal
– Benoit Sehba, University of Ghana
– Leonard Todjihounde, IMSP, Benin
– Hamidou Touré, University of Ouagadougou
Local Organizing Committee
– Antoine-Marie Bogso, Research Associate, AIMS Ghana
– Beauty Beatrice Kwawu, Programs Manager, AIMS Ghana
– Olivier Menoukeu Pamen, German Research Chair, AIMS Ghana and University of Liverpool
– Bernard Oduoku Bainson, Academic Manager, AIMS Ghana
– Prince Osei, Center President, AIMS Ghana
Application and Requirements
All inquiries should be sent via email to the Programme Manager, Beauty Beatrice Kwawu: beauty@aims.edu.gh.
The subject of your email should have your full name and the abbreviations of the workshop as shown in the
example: BeautyBeatriceKwawu_2MAP
Download Flyer here.
Application Closed.
Scheduled to be from 16th to 27th
August 2021 at AIMS Ghana in Accra.
Confirmed Lecturers
- Joseph Ansong, University of Ghana, Ghana
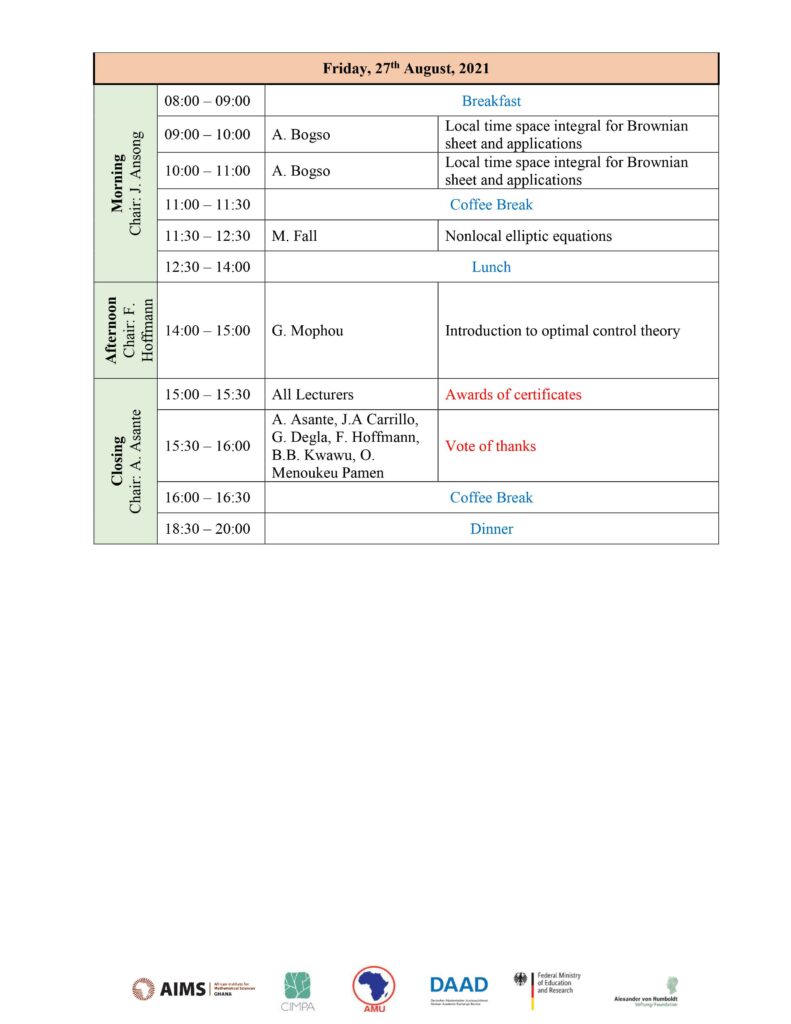
- Antoine-Marie Bogso, Research Associate, AIMS Ghana
- Almut Burchard, University of Toronto, Canada
- Jose A. Carrillo, University of Oxford, UK
- Sandra Cerrai, University of Maryland, US
- Guy Degla, IMSP Benin
- Mouhamed Moustapha Fall, AIMS Senegal, Senegal
- Thierry Goudon, INRIA Research Centre Sophia Antipolis, France
- Franca Hoffmann, California Institute of Technology, US Scientific Committee
- Ivan Moyano, Université Côte d’Azur, France
- Gisele Mophou, University of Antilles, Guadeloupe
- Ludovic Tangpi, Princeton University, US Advance Courses Lecturers
- Olivier Menoukeu Pamen: African Institute for Mathematical Sciences (AIMS) Ghana and University of Liverpool
Local Organising Committee
– Antoine-Marie Bogso, Research Associate, AIMS Ghana
– Beauty Beatrice Kwawu, Programs Manager, AIMS Ghana
– Olivier Menoukeu Pamen, German Research Chair, AIMS Ghana and University of Liverpool
– Bernard Oduoku Bainson, Academic Manager, AIMS Ghana
– Prince Osei, Center President, AIMS Ghana
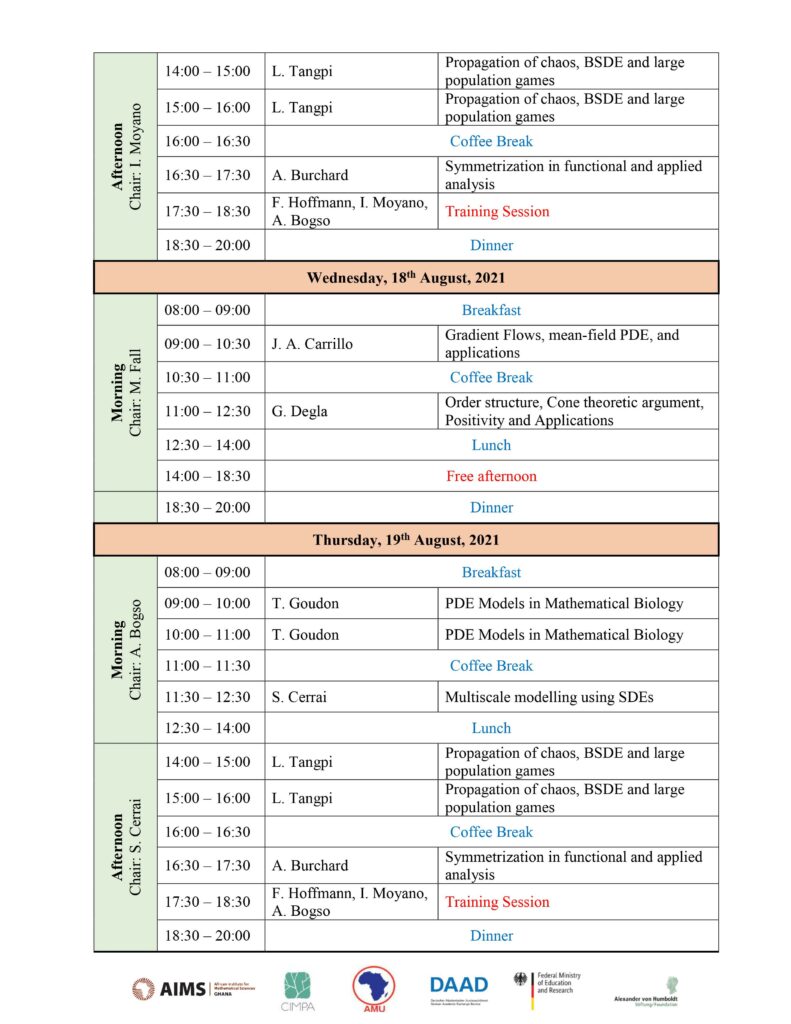
Lecturer: Sandra Cerrai
Affiliation: University of Maryland, US
Duration: 6 hours
Title: Multiscale modelling using SDEs
Abstract: We will discuss systems with multiple scales described by stochastic partial
differential equations. We will introduce basic aspects of this theory in order to connect to 7 interesting questions of research in this area such as the small noise asymptotics of those systems, their long time behavior, averaging phenomena, singular perturbation results and so on.
Lecturer: Thierry Goudon.
Affiliation: INRIA Research Centre Sophia Antipolis, France.
Duration: 6 hours
Title: PDE Models in Mathematical Biology
Abstract: The lecture is concerned with the mathematical modeling of biological phenomena. We will discuss how the mathematical framework can shed some light on these phenomena, paying a specific attention to asymptotic issues. Moreover, the models are amenable to numerical treatments; and we will present dedicated approaches to investigate on numerical grounds these equations.
Lecturer: Almut Burchard
Affiliation: University of Toronto, Canada
Duration: 6 hours
Title: Symmetrization in functional and applied analysis.
Abstract: Balls and spheres appear frequently as the solutions to geometric optimization problems. For example, they minimize surface area as well as electrostatic capacity among bodies of given volume. But on second thought, it is also common for minimizers of a radially symmetric problem to break the symmetry. We will discuss how symmetrization techniques can be used to find radially symmetric minimizers, for problems arising in
functional analysis and the physical sciences. The goal is to learn to see when these methods apply, when they should fail, and how to recognize possible symmetry-breaking.
Lecturer: Ludovic Tangpi.
Affiliation: Princeton University, US.
Duration: 6 hours
Title: Propagation of chaos, BSDE and large population games
Abstract: In probability theory and random dynamical systems, the propagation of chaos roughly refers to the asymptotic behaviour of (weakly) interacting particles systems for which initial chaotic configurations ”propagate” through time when the number of particles becomes infinitely large. In this course, we will review elementary
notions of propagation of chaos for stochastic differential equations and discuss some recent development. This will allow us to develop a theory of ”backward propagation of chaos” for backward stochastic differential equations and systems of coupled forward and backward stochastic differential equations. The third part of the course will be concerned with examples and applications. We will mostly consider examples from the theory of
large population games.
Lecturer: Jos´e A. Carrillo
Affiliation: Imperial College London, UK
Duration: 6 hours
Title: Gradient Flows, mean-field PDE, and applications
Abstract: I will discuss basic properties of gradient flows that can be generalized to the case of metric spaces such as probability measures. An introductory material of variational calculus in the setting of probability measures and optimal transport will be discussed. Applications to PDEs and mean-field limits will be covered in
detail. The PDE models will range from Keller-Segel type models for chemotaxis and models describing swarming to stochastic interacting particles leading to phase transitions.
Lecturer: Guy Degla.
Affiliation: IMSP Benin.
Duration: 1hour 30minutes.
Title: Order structure, Cone theoretic argument, positivity and applications.
Abstract: We shall introduce the general concept of positivity in connection with order structures on any nonempty set and with cones in Banach spaces. Positivity theory is motivated by the intrinsicness of the real world which usually constrains mathematical models to involve functions measuring empirical real magnitudes such as population or matter densities, temperatures, pressures and chemical concentrations. Moreover we shall show the interplay between order structure, cone theoretic argument and maximum principles in Partial Differential Equations. As applications, we shall consider existence, uniqueness and stability results concerning Fixed point problems of order preserving maps, Positive Eigenvalue Problems, Positive Dynamical Systems, Controllability and reachability of nonlinear discrete-time systems described by convex processes, Bifurcation theory, and Vector optimization.
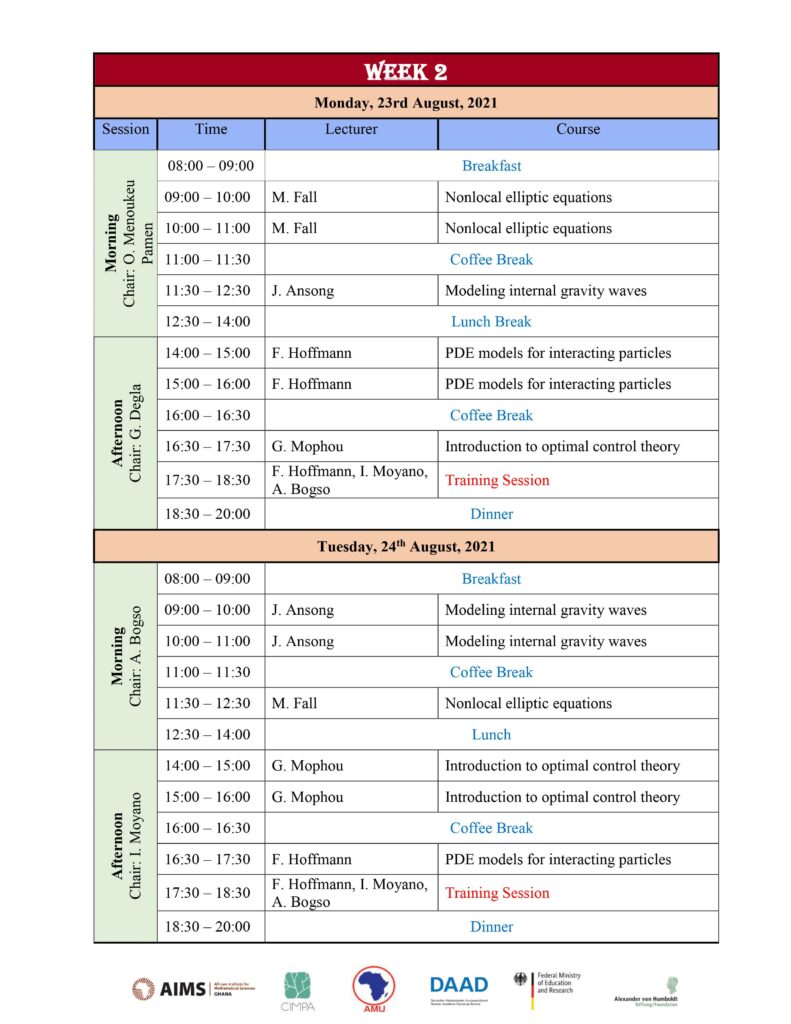
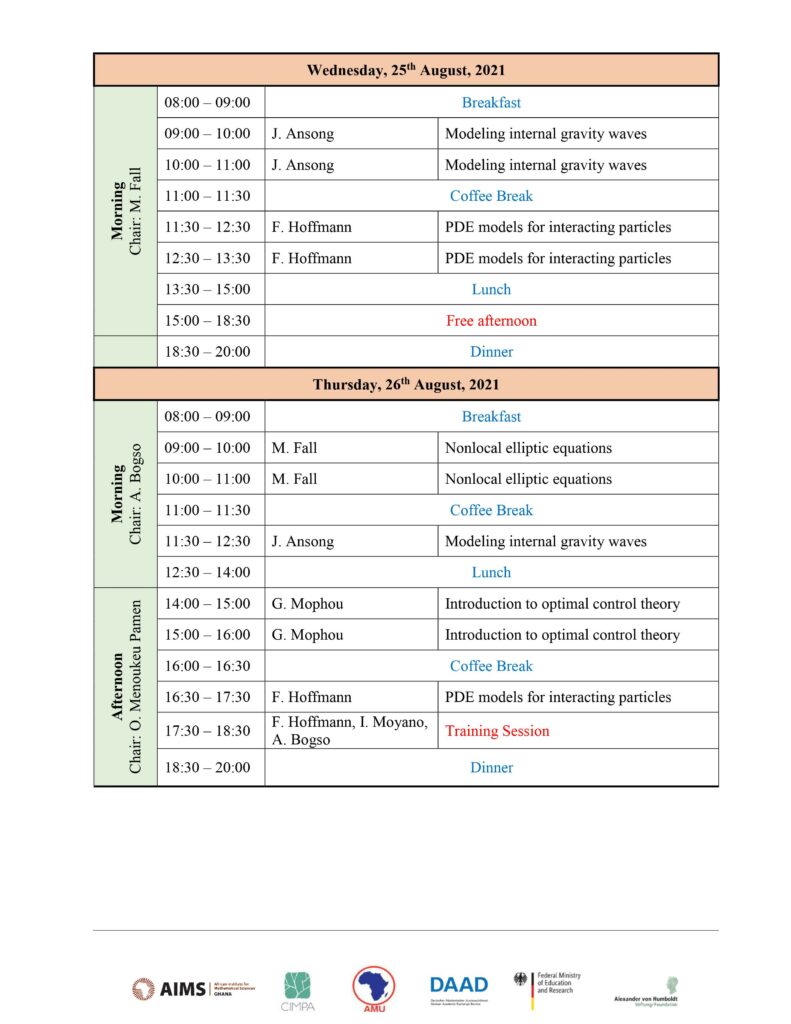
Lecturer: Mouhamed Moustapha Fall
Affiliation: AIMS Senegal, Senegal
Duration: 6 hours
Title: Nonlocal elliptic equations
Abstract: In recent years, the study of integrodifferential equations have attracted a lot of attention. Notably those of fractional type, which are toy models in L´evy processes. In the context of integrodifferential equations, L´evy processes play the same role that Brownian motion plays in the theory of second-order PDEs. They naturally arise in probability, geometry, quantum physics, phase transition theory and crystal dislocation
dynamics. The course will be an overview on qualitative analysis of such nonlocal problems and an introduction to nonlocal geometric problems. The course is intended for beginners in nonlocal equations.
Lecturer: Joseph Ansong
Affiliation: University of Ghana, Ghana
Duration: 1 hour 30minutes
Title: Modeling internal gravity waves
Abstract: High-resolution global hydrodynamical models that contain both eddies and internal waves are becoming increasingly useful for the SWOT satellite mission. It is therefore important to know how well such models compare to observations. Here we focus on the ability of four such models to reproduce the internal tide sea surface height signature seen in nadir altimeters. These include simulations from the HYbrid Coordinate Ocean Model (HYCOM), the Modular Ocean Model Version 6 (MOM6), the Nucleus for European Modelling of the Ocean (NEMO), and the Massachusetts Institute of Technology general circulation model (MITgcm). Consistent with a previous study that employed only the HYCOM model, we find that the absence of an explicit damping mechanism on tidal flows in global ocean models results in internal tides that are too energetic and propagate too far from their sources. We also find that the length of model output used in harmonic
analysis impacts the comparison of internal tide amplitudes to those derived from along-track satellite altimetry, consistent with the previous investigation. Differences in internal tide strength in different models run at the same resolution, and without additional explicit damping, are likely due to differences in numerics amongst the models, although further study is needed to confirm this. This study also documents, for the first time, some details of the tidal forcing in the particular MITgcm runs examined here, that adversely affect the accuracies of the modelled tides, and suggests correction factors using less expensive barotropic shallow-water simulations that roughly mimic the tidal forcing in the MITgcm runs.
Lecturer: Gisele Mophou.
Affiliation: Universit´e des Antilles, France.
Duration: 6h.
Title: Stackelberg-Nash null controllability for a nonlinear heat equation in an unbounded
domain.
Abstract: In this course, we will study the Stackelberg strategy for a nonlinear parabolic equation in an unbounded domain. We assume that we can act on the system by three controls hierarchically. Two controls called followers that provide a Nash quasi-equilibrium for two cost functionals. The third control named leader is supposed to bring the state of the system to rest at the final time. The results are achieved by means of observability inequality of Carleman type that we established for the adjoint systems and a fixed point theorem under the assumptions that the uncontrolled domain is bounded.
Lecturer: Franca Hoffmann
Affiliation: California Institute of Technology
Duration: 1hour 30minutes
Title: PDE models for interacting particles
Abstract: Partial differential equations appear across the applied sciences and engineering to model complex real-world phenomena. Especially non-linear and non-local terms pose challenges for the analysis of their solutions. We will look at different non-linear and non-local equations that model interacting particles, such as the porous medium equation for an isentropic gas, or collective behaviour models for animal groups. If one combines both non-linear and non-local terms in the same equation, new methods are needed to analyse their behaviour. We will look at the famous Patlak-Keller-Segel model for bacterial chemotaxis describing how cells communicate and interact with each other, leading to more general models representing competing effects of attractive and repulsive forces.



Centre International de Mathématiques Pures et Appliquées 
African Mathematical Unioin 
DAAD: German Academic Exchange Service 
Federal Ministry of Education and Research of Germany 
Alexander von Humboldt Foundation
For further enquiries, contact Beauty Beatrice Kwawu by email, telephone. The contact details are as follows:
African Institute for Mathematical Sciences (AIMS), Ghana
Summerhill Estates,
East Legon Hills – Accra, Ghana
Tel.: +233-206-116-215
E-mail: beauty@aims.edu.gh
For further enquiries, contact Beauty Beatrice Kwawu by email, telephone. The contact details are as follows:
African Institute for Mathematical Sciences (AIMS), Ghana
Summerhill Estates,
East Legon Hills – Accra, Ghana
Tel.: +233-24-3220-631
E-mail: beauty@aims.edu.gh.

