Conference on Mathematics and its Applications

CMIA Talk Abstracts

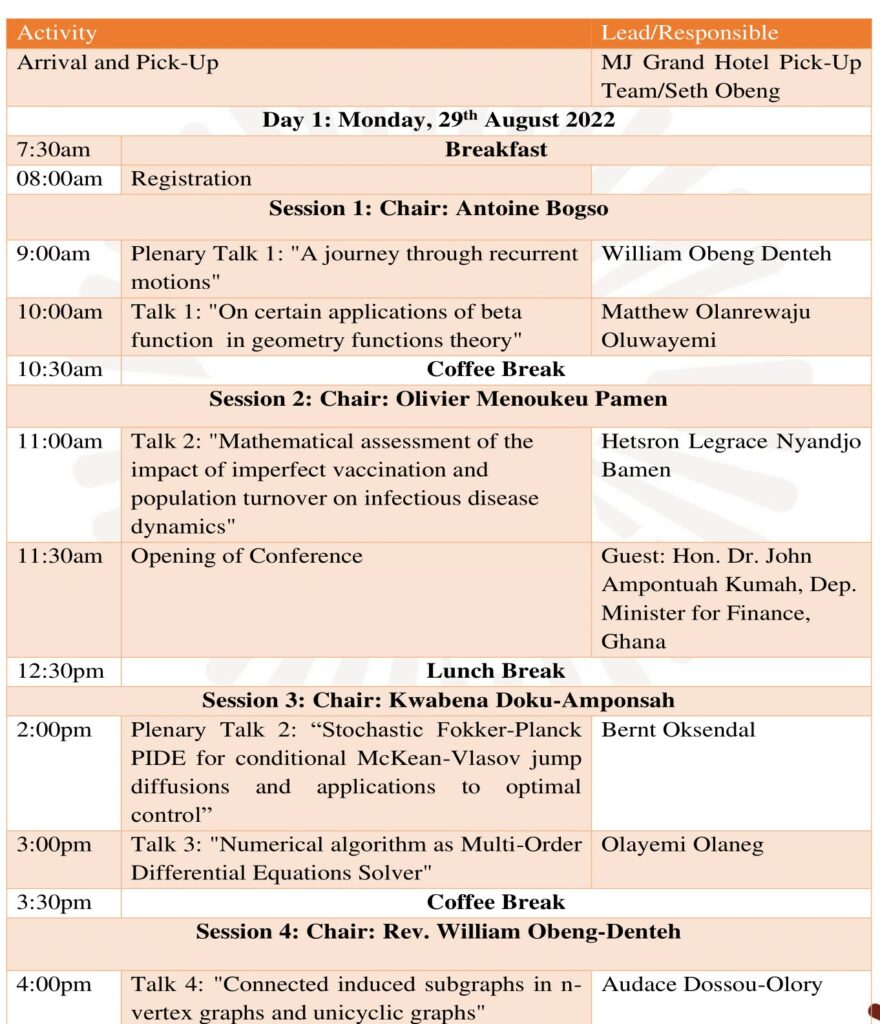
Day 1

Plenary Talk 1:  Obeng Denteh “A journey through recurrent motions”

Abstract: This is an exposition on the study of dynamical systems. One of our purposes is to acquaint ourselves with the Birkhoff Recurrence Theorem and to look at Poisson stable motion, recurrent motions and almost periodic motions.

Talk 1: Matthew Olanrewaju Oluwayemi “On certain applications of beta function in geometry functions theory”

Abstract: Geometric function theory (GFT) is a classical area of complex analysis with the aim of abridging the gap between analysis and applications. In this study, the authors introduced certain classes of univalent functions associated with an Eulerian integral known as beta function and studied some of the geometric properties.

Talk 2: Hetsron Legrace Nyandjo Bamen “Mathematical assessment of the impact of imperfect vaccination and population turnover on infectious disease dynamics”

Abstract: Vaccination is essential for the management of infectious diseases, many of which continue to pose devastating public health and economic challenges across the world. However, many vaccines are imperfect having only a partial protective effect in decreasing disease transmission and/or favouring recovery of infected individuals, and possibly exhibiting trade-off between these two properties. Furthermore, population turnover, that is the rate at which individuals enter and exit the population, is another key factor determining the epidemiological dynamics. While these factors have yet been studied separately, we investigate the interplay between the efficiency and property of an imperfect vaccine and population turnover. We build a mathematical model with frequency incidence rate, a recovered compartment, and an heterogeneous host population with respect to vaccination. We first compute the basic reproduction number $\mathcal{R}_0$ and study the global stability of the equilibrium points. Using a sensitivity analysis, we then assess the most influential parameters determining the total number of infected and $\mathcal{R}_0$ over time. We derive analytically and numerically conditions for the vaccination coverage and efficiency to achieve disease eradication ($\mathcal{R}_0 < 1$) assuming different intensity of the population turnover (weak and strong), vaccine properties (transmission and/or recovery) and trade-off between the latter. We show that the minimum vaccination coverage increases with lower population turnover, decreases with higher vaccine efficiency (transmission or recovery), and is increased/decreased by up to 15\% depending on the trade-off between the vaccine properties. We conclude that the coverage target for vaccination campaigns should be evaluated based on the interplay between these factors.

Talk 3: Olayemi Olanegan “Numerical algorithm as Multi-Order Differential Equations Solver”

Abstract: This research focuses on an innovative procedure of integrating higher-order systems of equations with initial values. The proposed 4-point implicit method constructed by collocation and interpolation procedures was used to integrate system of third, and fourth-order differential equations directly with a substantial enhancement in efficiency. The method derived in a block mode to simultaneously estimate three kind of differential equations has improved accuracy and rate of convergence in problem evaluations. The analysis of the scheme was established via order, consistency, zero-stability, and convergence. The proposed method was used to solve some systems of equations for third and fourth-order as numerical experiments to check the favorable performance of the method in comparison to some existing methods.

Talk 4: Audace Dossou-Olory “Connected induced subgraphs in n-vertex graphs and unicyclic graphs”

Abstract: Counting and understanding graph structures with particular properties has many applications, especially to network theory, computer science, biology and chemistry. For instance, graphs can represent biological networks at the molecular or species level (protein interactions, gene regulation, etc). The topological structure of an interconnection network is a connected graph where, for example, vertices are processors and edges represent links between them. In chemical networks, vertices are atoms and edges represent their bonds. An important question is to find all matches of a specific motif within a larger network (the subgraph isomorphism problem, or the induced subgraph isomorphism problem). Both cases are known to be in general NP-complete, although in some instances (such as planar graphs), efficient algorithms are available. A step to these problems usually consists of enumerating all possible subgraphs or induced subgraphs of the network. This talk discusses the number of connected induced subgraphs of a simple graph or unicyclic graph on n vertices with a particular emphasis on connected induced subgraphs. Specifically, I will be concerned with determining their minimum and maximum numbers, and also characterising the extremal graphs. Finally, I will mention some directions for future research.

Talk 5: Djideme Franck Houenou “Deformation retract of the group of symplectomorphisms”

Abstract: In this work, we study the dynamics of the group of symplectomorphisms under the mean curvature flow. We proved that the group retracts to the set of biholomorphic maps.

Plenary Talk 2: Bernt Oksendal “Stochastic Fokker-Planck PIDE for conditional McKean-Vlasov jump diffusions and applications to optimal control”

Abstract: The purpose of this paper is to study optimal control of conditional McKean-Vlasov  (mean-field) stochastic differential equations with jumps (conditional McKean-Vlasov jump diffusions, for short). To this end, we first prove a stochastic Fokker-Planck equation for the conditional law of the solution of such equations.  Combining this equation with the original state equation, we obtain a Markovian system for the state and its conditional law. Furthermore, we apply this to formulate an Hamilton-Jacobi-Bellman (HJB) equation for the optimal control of conditional McKean-Vlasov jump diffusions. 

Finally we apply these results to solve explicitly the following problems:

–  Linear-quadratic optimal control of conditional stochastic McKean-Vlasov jump diffusions.

– Optimal consumption from a cash flow modelled as a conditional stochastic McKean-Vlasov differential equation with jumps. The talk is based on joint work with Nacira Agram, KTH, Stockholm, Sweden.

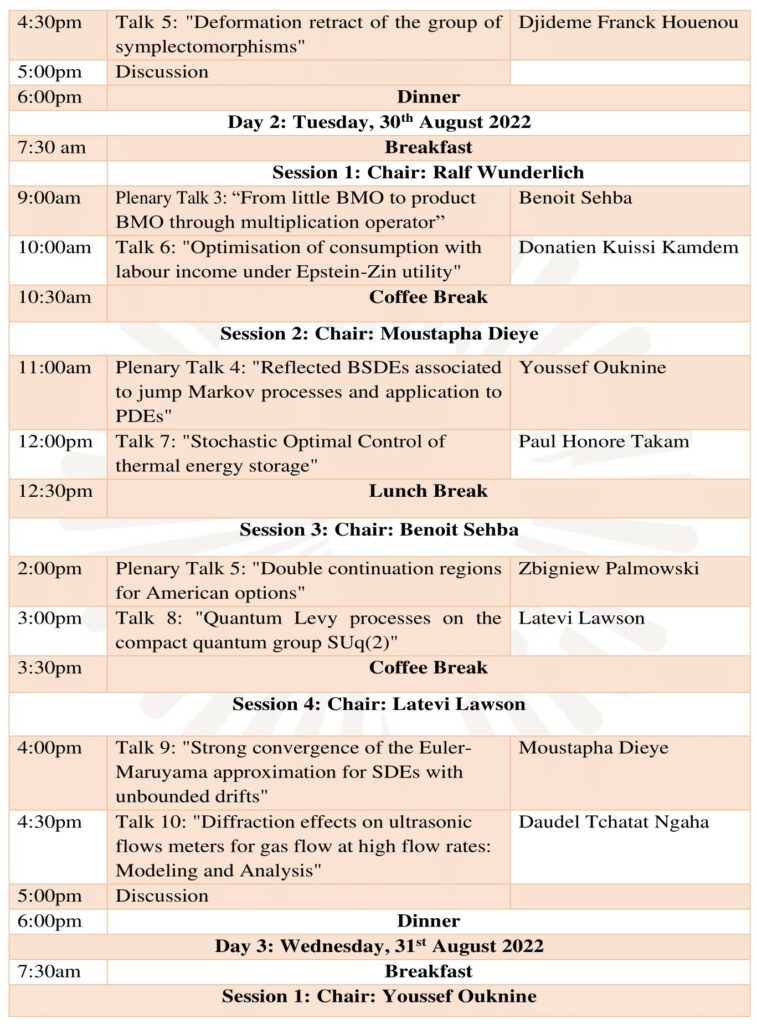
Day 2

Plenary Talk 3: Benoit Sehba “From little BMO to product BMO through multiplication operator.”

Abstract: We characterize the multipliers from the little BMO of Cotlar-Sadosky to the product BMO of Chang-Fefferman on the polydisk.

Plenary Talk 4:  Youssef Ouknine “Reflected BSDEs associated to jump Markov processes and application to PDEs”

Abstract: In this paper, we study a class of reflected backward stochastic differential equations (RBSDE) driven by the compensated random measure associated to a given pure jump Markov process X on a general state space U. The “reflection” keeps the solution above a given càdlàg process. We prove the uniqueness and existence both by a combination of the Snell envelope theory and fixed-point argument. We apply these results to represent probabilistically the value function of some quasi-variational inequalities associated to the Markov process X.

Plenary Talk 5:  Zbigniew Palmowski “Double continuation regions for American options”

Abstract: We consider the Lévy model of the perpetual American call and put options with a negative discount rate. We will consider the continuous observation case as in De Donno et al. (2020) and the Poisson observation case as in Palmowski et al. (2021). In both cases the stopping region that characterizes the optimal stopping time is either a half-line or an interval. The objective of this talk is to obtain explicit expressions of the stopping and continuation regions and the value function, focusing on spectrally positive and negative cases. To this end, we compute the identities related to the first Poisson) arrival time to an interval via the scale function and then apply those identities to the computation of the optimal strategies. We also discuss the convergence of the optimal Poisson solutions to those in the continuous observation case as the rate of observation increases to infinity. Numerical experiments are also provided. The talk is based on joint papers with Marzia De Donno, José Luis Pérez, Joanna Tumilewicz, and Kazutoshi Yamazaki.

Talk 6: Donatien Kuissi Kamdem “Optimisation of consumption with labour income under Epstein-Zin utility”

Abstract: Classical problems in mathematical finance include portfolio optimisation problems where an investor seeks to maximise the expected utility of her instantaneous consumption and terminal wealth. In this work we extend Merton’s original problem of optimal consumption and portfolio choice in continuous time to consider an agent who receives a stochastic income and is subjected to liquidity constraint. The liquidity constraint considered is the nonnegative wealth constraint, often called the borrowing constraint, and stands to be one of the most important economic constraints on portfolio selection problems. We investigate the problem using convex duality approach with a utility of Epstein-Zin type.

Talk 7: Paul Honore Takam “Stochastic Optimal Control of thermal energy storage”

Abstract: Climate change and the turnaround in energy policy require the improvement of energy efficiency in all areas. Thermal storage facilities help to mitigate and to manage temporal fluctuations of heat supply and demand for heating and cooling systems of single buildings as well as for district heating systems. We focus on a heating system equipped with several heat-production units using also renewable energies and an underground thermal storage. The thermal energy is stored by raising the temperature of the soil inside the storage. It is charged and discharged via heat exchanger pipes filled with a moving fluid. Besides the numerous technical challenges and the computation of the spatiotemporal temperature distribution in the storage also economic issues such as the cost-optimal control and management of such systems play a central role. The latter leads to challenging mathematical optimization problems. There we incorporate uncertainties about randomly fluctuating renewable heat production, environmental conditions driving the heat demand and supply. The dynamics of controlled state process is governed a PDE, a random ODE driving by the difference between supply and demand, and the SDEs. Model reduction techniques are adopted to cope with the PDE describing the spatio-temporal temperature distribution in the geothermal storage. Finally, time-discretization leads to a Markov decision process for which we apply numerical methods to determine a cost-optimal control.  This is a joint work with Ralf Wunderlich (BTU Cottbus-Senftenberg) and Olivier Menoukeu Pamen (AIMS Ghana, University of Liverpool).

Talk 8:  Latevi Lawson “Quantum Levy processes on the compact quantum group SUq(2)”

Abstract: Quantum Lévy processes on a quantum group are, like classical Lévy processes with values in a Lie group, classified by their infinitesimal generators. We derive a formula for the infinitesimal generators on the quantum group SUq(2) and decompose them in terms of an infinite-dimensional irreducible representation and of characters. Thus, we obtain a quantum Lévy Khintchine formula and we derive the corresponding Hunt formula.

Talk 9: Moustapha Dieye “Strong convergence of the Euler-Maruyama approximation for SDEs with unbounded drifts”

Abstract: In this work, we prove strong convergence on small time interval of order 1=2-\epsilon for arbitrarily small \epsilon > 0 of the Euler-Maruyama Holder continuous approximation for additive Brownian motion with Holder continuous drift. The proof is based on direct estimations of functional of the Euler-Maruyama approximation.  The order of convergence does not depend on the Holder index of the drift, thus generalizing the results obtained in [10] to both Linear growth and to an optimal convergence order.

Talk 10: Daudel Tchatat Ngaha “Diffraction effects on ultrasonic flows meters for gas flow at high flow rates: Modeling and Analysis”

Abstract: The improvement in the accuracy of flow rate measurements of oil and gas has been going back for decades and is useful for industrial applications. Today they are generally accepted by and widely used in industry. As the technology has matured, the accuracy and stability of the flow meters have gradually improved. Looking ahead, there is a trend in the industry of more remote and subsea operations. This means that the flow meters need to be capable of more stand-alone operations where flow calibrations of the meters will be quite costly. One effect that has been studied in order to make the ultrasonic flow meters more robust and accurate is the diffraction effect. Due to the finite size of the two ultrasonic transducers, an acoustic beam is generated when the ultrasonic signal is propagating between the transducers, and the transit times measured between the transducers are affected by this. This present work deals with the modelling of sound propagation in moving medium with applications in flow rate measurement and proposes an understanding of diffraction effects for acoustic beams propagating through a homogeneous flowing fluid to improve the accuracy of the ultrasonic flow meter. The study is oriented on mathematical modelling and numerical solution of the partial differential equations that are based on the fundamental hydrodynamic equations (Navier-Stokes Equations) and describe such a sound propagation. Results from such a study will be used as input for development of updated flow algorithms/equations.

Day 3

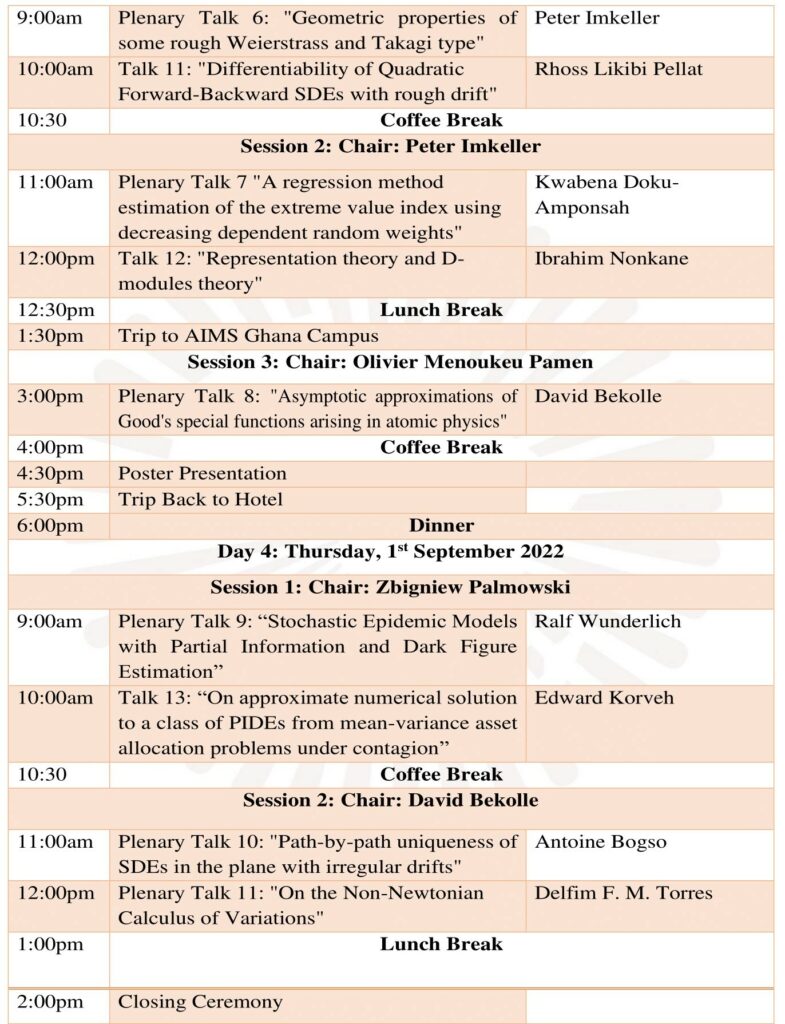
Plenary Talk 6: Peter Imkeller  “Geometric properties of some rough Weierstrass and Takagi type”

Abstract: We investigate geometric properties of graphs of Weierstrass or Takagi type functions, represented by series based on smooth functions. They are H ̈older continuous, and can be embedded into smooth dynamical systems, where their graphs emerge as pullback attractors. It turns out that occupation measures and Sinai-Bowen-Ruelle (SBR) measures on their stable manifolds are dual by time reversal. A suitable version of approximate self-similarity for deterministic functions allows to ”telescope” small scale properties from macroscopic ones. As a consequence, absolute continuity of the SBR measure is seen to be dual to the existence of local time. The link between the rough curves considered and smooth dynamical systems can be generalized in various ways, for instance by randomization to individual Brownian trajectories. Applications to regularization of singular ODE by rough signals are on our agenda. This is joint work with O. Pamen (U Liverpool and AIMS Ghana) and G. dos Reis (U Edinburgh).

Plenary Talk 7: Kwabena Ndoku-Amponsah “A regression method estimation of the extreme value index using decreasing dependent random weights”

Abstract: In this talk, a regression method for the extreme value index of a Pareto-type distribution is presented using the weighted least squares approach. We show that the proposed estimator is consistent, asymptotically normal, and unbiased considering the second-order assumption on the data distribution.

Plenary Talk 8: David Bekolle “Asymptotic approximations of Good’s special functions arising in atomic physics”

Abstract: We study various asymptotic approximations of Good’s special functions arising in atomic physics. These special functions are situated beyond Anger’s functions to which they are closely related. The functions under study depend on two variables, and present themselves as oscillatory integrals, with the phase depending on one of the variables and the amplitude on the other one. We will use the method of the stationary phase, but this one does not suffice to describe the behavior in all cases.

Talk 11: Rhoss Likibi Pellat “Differentiability of Quadratic Forward-Backward SDEs with rough drift”

Abstract: In this talk, we consider quadratic forward-backward SDEs (QFBSDEs), for which the drift in the forward equation does not satisfy the standard globally Lipschitz condition and the driver of the backward system possesses nonlinearity of type f(|y|)|z|^2, where f is any locally integrable function. We prove both the Malliavin and classical derivative of the QFBSDE and provide representations of these processes. We study a numerical approximation of this system in the sense of (Imkeller-Dos Reis, 2010) in which the authors assume that the drift is Lipschitz and the driver of the BSDE is quadratic in the traditional sense (i.e., f is a positive constant). We show that the rate of convergence is the same as in (Imkeller-Dos Reis, 2010)

Talk 12: Ibrahim Nonkane “Representation theory and D-modules theory”

Abstract: A prevailing idea in representation theory is that larger structures can be understood by breaking them up into their smallest pieces. Also the natural framework of algebraic geometry is one of the polynomials and, the development of modern algebra has given a particular status to polynomials. In this vein, we study polynomial rings as modules over a ring of invariant differential operators by elaborating its irreducible submodules. The D-module direct image of an irreducible holonomic module with regular singularities under a proper map is semi-simple according to the decomposition theorem. The simplest case is when the map  π : X = specB → Y = specA is finite, and the module is the structure sheaf $B = O_X$ . Then an elementary and whollyalgebraic proof exists, using essentially the ordinary Galois group G of the function field extension corresponding to π. This proof uses that the irreducible D-submodules of $π_+(O_X)$ are in one-to-one correspondence with irreducible representations of G.  In this talk, we study the decomposition sttructure when when G is the symmeric group,and when G is the generalized symmetric group.

Day 4

Plenary Talk 9: Ralf Wunderlich “Stochastic Epidemic Models with Partial Information and Dark Figure Estimation”

Abstract: Mathematical models of epidemics such as the current COVID-19 pandemics often use compartmental models dividing the population into several compartments. Based on a microscopic setting describing the temporal evolution of the subpopulation sizes in the compartments by stochastic counting processes one can derive macroscopic models for large populations describing the average behavior by associated ODEs such as the celebrated SIR model. Further, diffusion approximations allow to address fluctuations from the average and to describe the state dynamics also for smaller populations by stochastic differential equations (SDE). Usually not all of the state variables are directly observable and we are facing the so-called “dark figure” problem addressing for example the unknown number of asymptomatic and non-detected infections. Such not directly observable states are problematic if it comes to the computation of characteristics of the epidemic such as the effective reproduction rate and the prevalence of the infection within the population. Further, the management and containment of epidemics relying on solutions of (stochastic) optimal control problems and the associated feedback controls need observations of the current state as input. The estimation of unobservable states based on records of the observable states leads to a non-standard filtering problem for partially observable stochastic models. We adopt the extended Kalman filter approach coping with nonlinearities in the state dynamics and the state-dependent diffusion coefficients in the SDEs. This allows to develop approximative solutions to that filtering problem. Numerical results illustrating our theoretical finding are presented. This is joint work with Florent Ouabo Kamkumo, Ibrahim Mbouandi Njiasse (Cottbus) and Olivier Menoukeu Pamen (AIMS Ghana/Liverpool).

Plenary Talk 10: Antoine Bogso “Path-by-path uniqueness of SDEs in the plane with irregular drifts”

Abstract: We study path-by-path uniqueness for multidimensional stochastic differential equations driven by the Brownian sheet. We assume that the drift coefficient is unbounded, verifies a spatial linear growth condition and is the difference of componentwise nondeacreasing functions. Our approach consists of showing the result for bounded drifts that are difference of componentwise nondecreasing functions using both a local time-space representation and a law of iterated logarithm for Brownian sheets. The desired result follows using a Gronwall type lemma on the plane.  As a by-product, we obtain the existence of a unique strong solution of multidimensional SDEs driven by the Brownian sheet when the drift is the difference of two (componentwise) non-decreasing functions and satisfies a spatial linear growth condition. This is a joint work with Olivier Menoukeu-Pamen (AIMS Ghana, University of Liverpool).

Plenary Talk 11: Delfim F. M. Torres “On the Non-Newtonian Calculus of Variations”
Abstract: The calculus of variations is a field of mathematical analysis  born in 1687 with Newton’s problem of minimal resistance, which is concerned with the maxima or minima of integral functionals. Finding the solution of such problems leads to solving the associated Euler-Lagrange equations. The subject has found many applications along the centuries, e.g., in physics, economics, engineering, and biology. Up to this moment, however, the theory of the calculus of variations has been confined to Newton’s approach to calculus. Because in many applications negative values of admissible functions are not physically plausible, we propose an alternative calculus of variations based on the non-Newtonian approach first introduced by Grossman and Katz in the period between 1967 to 1970, which provides a calculus defined, from the very beginning, for positive real numbers only, and is based on a (non-Newtonian) derivative that permits to compare relative changes between a dependent positive variable and the independent variable that is also positive. In this way, the non-Newtonian calculus of variations we introduce provides a natural framework for problems involving functions with positive images. The new calculus of variations complements the standard one in a nontrivial/multiplicative way, guaranteeing that the solution remains in the physically admissible positive range.

Talk 13: Edward Korveh “On approximate numerical solution to a class of PIDEs from mean-variance asset allocation problems under contagion.”

Abstract: In this talk, we present an approximate numerical solution to a class of partial integro differential equations (PIDEs) resulting from mean-variance asset allocation problems under contagion. We use the finite difference method for the differential part and a generic numerical integration scheme for the integral part. We present computer simulated results for some special cases.

Download