Conference on Mathematics and its Applications – 2023

CMIA 2023 Talk Abstracts

Day 1

Name: Felix Shu

Title: On an autoregressive process driven by a sequence of weakly independent and identically distributed cylindrical random variables Σ

Abstract: Let {Zn} n∈Z be a sequence of weakly independent and identically distributed cylindrical random variables in a Banach space U and A be a bounded linear operator on U.We show that under conditions, for each n ∈ Z, the series

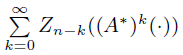
converges in C2 and if we define Yn for each n by

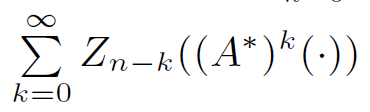
then the cylindrical process {Yn}n∈Z solves the cylindrical difference equation Xn = AXn−1 + Zn. We prove analogues of statements which hold for similar processes in Euclidean space.

When {Zn} is a sequence of weakly Gausian cylindrical random variables, the cylindrical distribution of Yn is shown to be weakly Gaussian and independent of n and conditions are given under which {Yn} is unique.

Name: Michael Manford

Title: An Alternative Multivariate Exponential Power Distribution

Abstract: In the existing Multivariate Exponential Power Distribution (EPD), the shape parameter has the tendency to affect the variability in the data leading to distorted features of the distribution. This study resolves this problem by obtaining a generalized expression in place of the constant coefficient (0.5) of the quadratic form of the Multivariate EPD as a function of the shape parameter, such that the variance-covariance matrix of the data is exactly equal to the scale parameter. The density function thus obtained is a more generalized Multivariate EPD that provides flexibility in depicting the true underlying characteristics of the distribution for all sample sizes.

Name: Ghislaine Flore Kabadiang

Title: Cubic Complex Ginzburg Landau Equation in a Doped Nonlocal Optical Fiber

Abstract: Considering the theory of electromagnetic waves from the Maxwell’s equations, we introduce an extended (3+1)D cubic complex Ginzburg-Landau equation describing the dynamics of dissipative light bullets in optical fiber amplifiers under the interplay between dopants and a spatially nonlocal nonlinear response. The model equation that is derived includes the effects of the gain saturation, gain dispersion, fiber dispersion, fiber nonlinearity, atomic detuning, diffractive transverse effects, and nonlocal non-

linear response. A system of eight coupled ordinary differential equations for the amplitude, temporal and spatial pulse widths, and position of the pulse maximum, unequal wavefront curvatures, chirp parameters, and the phase shift is derived on the basis of the variational technique. The obtained variational equations are integrated numerically, which allows us to investigate the evolution of the Gaussian beam along a doped nonlocal optical fiber.

Keywords: Spatio temporal dynamics, cubic-quintic nonlinearity, Light bullets non locality, non local optical fiber, variational approach.

Name: Rev. William Obeng-Denteh

Title: Mathematical Chaos Theory

Abstract: The Mathematical Chaos Theory represents a fascinating and interdisciplinary field of study that explores the inherent unpredictability and complexity within deterministic systems. Originating from the pioneering work of mathematicians such as Edward Lorenz, this theory has found applications across various scientific domains, including physics, biology, economics, and meteorology. This presentation provides an overview of the key principles of chaos theory, emphasizing the sensitivity to initial conditions, the concept of strange attractors, and the emergence of fractal patterns. This exploration into the Mathematical Chaos Theory not only enriches our theoretical foundations but also holds promise for practical applications in fields as diverse as cryptography, information theory, and the modeling of complex natural phenomena.

Name: Desmond Kofi Boateng

Title: Comparative Analysis of SVD-Based Methods for Image Compression

Abstract: The use of singular value decomposition based methods for image and video compression has generated significant attention due to their ability to achieve high quality compression while preserving the quality of the image and video. This study investigates the applications of singular value decomposition (SVD) for image and video compression using Julia, a high performance programming language for techinical computing. This research explore the mathematical foundations of SVD

and some variants such as the truncated SVD, the randomized SVD and the compressed SVD, and their potential for efficient compression of images and videos. Implementation of these methods in Julia and evaluation of the performances of the methods is done to assess the computational efficiency and the compression performance.

Name: Adekunle Kolawole

Title: Predictive Model for Students Academic Performance Using Generative Artificial Intelligence

Abstract: The educational landscape is evolving with the integration of artificial intelligence into various aspects of teaching and learning. This paper presents a novel approach to predicting students’ academic performance by harnessing the power of Generative Artificial Intelligence (GAI). In an era where data-driven decision-making is paramount, our predictive model employs cutting-edge GAI techniques to analyze diverse educational data sources, including historical performance records, student behavior patterns, and curriculum content. By combining generative models such as GANs and LSTM-based sequence prediction, our model will creates a dynamic and adaptive framework that not only forecasts academic outcomes but also generates personalized interventions for struggling students. We evaluate the performance of our model on real-world educational datasets and demonstrate its ability to provide timely insights into students’ progress, enabling educators to implement targeted interventions and improve learning outcomes. This research will contribute to the advancement of AI-driven education and underscores the potential of GAI in revolutionizing the way we support students in their academic journeys.

Name: Richard Kwame Ansah

Topic: Phase Transition In AI-Human Interaction Using Quartic Mean-Field Ising Model

Abstract: The presence of artificial intelligence (AI) machines in our society offers both opportunities and potential risks. To better understand this dynamic, we propose a simulation model for the Human-AI ecosystem. This model considers various factors, including biased actions among agents, interactions between peers, and interactions involving three or even four agents. The latter includes scenarios where three humans interact with an AI agent, two humans interact with two AI agents, or three AI agents interact with a human. Our primary objective is to explore how the proportion of AI agents in the ecosystem influences its behaviour. Our analysis provides compelling evidence that even a slight shift in the percentage of AI agents can result in significant and profound changes within the system. These changes could push the system towards one of two distinctly opposing states or leave it in an indeterminate state.

Day 2

Name: Youssef Ouknine

Title: Reflected and Doubly RBSDEs with Irregular Obstacles and a Large Set of Stopping Strategies

Abstract: We introduce a new formulation of reflected BSDEs and doubly reflected BSDEs associated with irregular obstacles. The first part of our work extends the classical optimal stopping problem to a broader set of stopping systems, namely the set of split stopping times, allowing for irregular payoff processes $\xi$ and a general filtration. The use of split stopping times enables a flexible representation of financial contracts and derivatives that rely on multiple conditions or triggers, and stochastic processes featuring jumps and other discontinuities.} We show that the value family can be aggregated by an optional process $v$, which is characterized as the Snell envelope of the reward process $\xi$ over split stopping times. Using this, we prove the existence and uniqueness of a solution $Y$ to irregular reflected BSDEs. In the second part of the paper, motivated by the classical Dynkin game with completely irregular rewards considered by Grigorova et al. (2018), we generalize the previous equations to the case of two reflecting barrier processes.

Name: Amina Salifu

Title: Data Transmission Reduction in IoT Wireless Sensor Networks.

Abstract: A Wireless Sensor Network (WSN) is a collection of spatially separated and specialized sensors that work together to monitor, record, and transmit information about the physical state of the environment to an internet-based location. In order to improve WSN power consumption, this work proposes a classification technique where K nearest neighborhood was applied in those clusters to select the best nodes. The purpose of the classification technique is to divide the network into various node groupings. We calculated the correlation matrix for one node in each group and cluster, and we also applied the RNN model to get a better prediction within each node in each cluster, so only one node of data will be sent from each cluster to the base station. Furthermore, the experimental results reveal that, based on a suitable choice of nodes, our proposed model performs accurate predictions, with minimum error measured using the Root Mean Squared Error (RMSE) as compared to related work. The radio-energy transmission model used in this work also shows that our proposed model is able to save two times more energy than most of the existing data transmission models.

Name: Rhoss Likibi Pellat

Title: Path-regularity of Path-dependent Quadratic FBSDEs with Dini-continuous drift

Abstract: In this talk, we prove that the L^2 regularity of the martingale integrand of the control process $Z$ remains valid for a large class of quadratic Markovian BSDEs with path-dependent functional terminal value having non-uniform Cauchy-Lipschitz drivers and rough drift coefficient.

Name: Latévi Mohamed Lawson

Title: Path integral in quasi-Hermitian position-deformed Heisenberg algebra with maximal length

Abstract: Non-Hermitian Hamiltonians with real spectra motivated remarkable research activities in quantum physics. Position deformation of an ordinary Heisenberg algebra with both maximal length and minimal momentum uncertainties demonstrated a loss of a Hermicity of operators that generate this algebra. Consequently, the Hamiltonian operator that involves these operators are also not Hermitian. In the present paper, with an appropriate positive-definite Dyson map, we establish the Hermicity of these operators by means of a quasi-similarity transformation. We then construct Hilbert space representations associated to these quasi-Hermitian operators that generate a quasi-Hermitian Heisenberg algebra. Finally, with the help of these representations we study the path integral of a free particle within this quasi-Hermitian algebra. We show that the action which describe the classical trajectories of both systems are bounded by the ordinary ones of classical mechanics. Consequently, particles of this system travel faster in this deformed Euclidean from one point to another with low kinetic energy.

Name: Jules Sadefo

Title: Risk-adjusted performance and semi-moments of non-Gaussian portfolio return distribution

Abstract: In this paper, we find analytic expressions of the lower partial moment and kappa index of linear portfolios when the returns are elliptically distributed. We also introduced the notion of Target Semi-Kurtosis of portfolio return and discuss the robust optimization Mean-LPM problem with nongaussian risk factors. Special attention is given to the particular case of a mixture of multivariate t-distributions with application for portfolio allocation of some ESG indices and the CAC 40 index.

Name: Hussein Salifu

Title: A Bayesian Non-Parametric Generalized Linear Mixed Model for Clustering and Prediction of Disease Outcome

Abstract: In this current work, we adopted a novel approach within the generalized linear mixed model

framework in which random effects are grouped or clustered without constraining profiles assignment to the same cluster which shares the same random effect parameter value. We achieved this by clustering profiles based on model parameters since model parameters are determined by data and the assumed model. In that case, individuals or units with similar covariates and responses would have similar parameter values as well. This was achieved by placing a Dirichlet process prior on the mean of a normal distribution from which the random effects parameters were drawn. The method was tested on simulated data. In simulations, we have shown that the method manages to recover the correct number of clusters, successfully cluster profiles, and correctly estimate model parameters.The approach has been implemented using the standard Bayesian modeling software PReMiuM. Similar methods have been proposed for longitudinal data with continuous responses. This paper extends these models in novel ways to clustered and longitudinal data, where the distribution of the response variable can be any member of the exponential family.

Keywords: longitudinal data; Dirichlet Process, clustering, Bayesian analysis; PReMiuM

Name: Mark Dadzie

Topic: Mathematical modeling and anlalysis of mycolactone toxin kinetics in Buruli Ulcer

Abstract: Buruli Ulcer is one of the neglected tropical disease that mostly affect people living in the rural areas. The evasive nature of the disease, when treatment is delayed results in loss of body part such as the limbs, legs, or arms as well as deformations in some parts of the body. This amputation or deformities left on patients coupled with the long period of time for treatment depending on the degree of lesion brings to bear economic hardships on treated and non-treated Buruli Ulcer patients. Several research works have been conducted on the possible modes of transmission in recent times — although the exact mode of transmission is not known — using mathematical models. However, using mathematical models to depict the kinetics of the toxin released by the Mycobacterium ulcerans, the causative bacterium for Buruli Ulcer has gained little or no attention in recent times. In this study, we improved on an existing system of time dependent partial differential equations that depicts the action of the mycolactone toxin in the subcutaneous tissues of Buruli Ulcer patients and presents qualitative analysis on the inaction of the MU after entering the skin as well as some numerical simulations. This research contributes to a better understanding of Buruli Ulcer and offers valuable insights for improving treatment strategies and reducing the disease’s impact on affected communities.

Name: Monica Veronica Crankson

Title: Optimal Control And Stability Analysis Of Bacterial Meningitis Model With Education And Vaccination

Abstract: This research presents a deterministic epidemic model for bacterial meningitis. The model is extended into an optimal control problem by incorporating two control measures; vaccination and educational campaign. The existence of the optimal control solution is proven and the necessary conditions required for an optimal control with respect to the proposed model was established using Pontryagin’s Maximum Principle. The Forward-Backward Sweep Method was used to carry out the numerical simulation via MATLAB. The results from the numerical simulation showed the effectiveness of each of the control strategies in controlling the prevalence of bacterial meningitis. Thus, the best and also an effective control strategy will be a combination of vaccination and educational campaigns.

Day 3

Name: Juma Kasozi

Title: Ruin and Optimal Control in an Insurance Portfolio

Abstract: The classical Cramer-Lundberg model represents the dynamics of the surplus of an Insurance company. The positive interest rate in the market forces the company to go for investments of the black and scholes type. In this talk, I will present variations of this basic model compounded by investments and study the resulting models for probability of ultimate ruin, maximal dividend payouts using a barrier strategy and optimal proportional re-insurance. The talk shall end with current research trends in the same context.

Name: Steve Springer Laryea

Title: Investors Trading Psychology, Asset Selection and Portfolio Optimisation in the Cryptocurrency Market; A Behavioural Perspective.

Abstract: This paper aims to investigate investors’ prospects in adding value to their portfolios by considering investors’ behavioural scores (Cumulative Prospect Theory (CPT) score) and a clustering technique in the selection of assets. The universe of assets constitutes 63 cryptocurrencies sourced from Bloomberg from Jan 01 2020 to May 31 2022 with a daily frequency. The study period was further segmented into two distinct and mutually exclusive periods, namely COVID – 19, and post – COVID – 19 for the purposes of the empirical analysis. Using the Differential Evolution algorithm (DE) for the optimisation, the results show that during the COVID – 19 period, portfolios of assets with lower CPT scores outperformed counterpart portfolios with higher CPT scores. However, during the post – COVID – 19 and Full sample periods, portfolios of assets with higher CPT scores outperformed similar portfolios with lower CPT. Generally, a clustered CPT-based portfolio produced the best optimisation results. These

findings provide intuitive and coherent investment strategies aimed at guiding investors in the cryptocurrency market.

Keywords: Cumulative Prospect Theory, Portfolio Optimisation, Differential Evolution, Clustering, COVID – 19, Cryptocurrency Market, Investors Behaviour.

Name: Nelson Christopher Dzupire

Title: An Optimal Investment Consumption Model for Retirees with no Health Insurance

Abstract: Retirees meet a number of problems as they are growing older which needs persistent attention. Hence, without a doubt, the outcomes of the financial markets influence the choices that people make when nearing retirement. In our model, the stock price dynamics follow Geometric Brownian motion (GBM) and our goal was to optimize the expected discounted utility of consumption and terminal wealth whilst considering health expenses. The investment return process comprises risk free asset and risky assets, and the health expenses. We choose power utility functions where comprehensive solutions for Hyperbolic Absolute Risk Aversion (HARA) utility functions are obtained and optimal investment, consumption and health expenditure strategies are derived by applying dynamic programming and variable change technique on the Hamilton-Jacobi-Bellman (HJB) equations. In our numerical results it showed various effects of some economic and market parameters on the optimal investment, consumption and health expense strategies. The inflation price market risk governs the amount invested in stock, bond and also how much to be put in health to sustain a given period of the retiree’s lifetime. As the health welfare rate R increases, the proportion of wealth invested in the stock increases. We also investigated the effects of the high correlation coefficients and low correlation coefficients on consumption and income rate respectively. As the constant variance discounting coefficient increases, seasoned enterprise annuity retirees decrease their allocation to risky assets. Finally, a numerical example is presented to depict the effects of financial parameters on the optimal investment strategy with health expenditure.

Name: Elizabeth Dadzie

Title: Pricing Weather-linked Insurance Derivatives for Agricultural Goods

Abstract: Weather derivatives are simply futures contracts or options on those contracts where the underlying commodity is a weather index. Insurance derivatives that are dependent on the weather are fast-rising as they have many applications and uses. The recent phenomenon of climate change has led to many uncertainties (weather) for farmers. We examine commodity (agricultural goods) yields that depend on weather factors such as temperature, rainfall, etc. We consider a farmer who wants to purchase an insurance derivative to mitigate the weather risk from an agent (insurer). This insurance derivative depends on some weather factors namely temperature and rainfall. The question we ask ourselves is, what is the fair price for this insurance product? We find this price under the risk neutral measure and present possible extensions to the physical measure and pricing via classical exponential utility. We also present some numerics on the weather factors and numerics for this pricing equation.

Name: Houénafa Clarisse Dete

Title: Relative performance of model selection criteria for Cox Proportional Hazards regression based on Kullback’s Symmetric Divergence.

Abstract: Survival analysis is a time-to-event analysis. There are several models used to analyze such data. The decision on the most suitable model for those data is an essential analysis point. For this purpose, different model selection criteria can be used under different assumptions. The aim of this study is to assess the performance of new model selection criteria based on Kullback’s Symmetric Divergence in the Cox Proportional Hazard model. We compared Akaike Information Criterion (AIC), corrected AIC, Bayesian Information Criterion, Kullback Information Criterion (KIC), corrected KIC (KICc) using the simulation study. Simulations were run using various combinations of the following: sample size n = 30, 50, 100, 200, 300, percent censoring C = 5%, 10%, 15%, 20%, 25%, 30% and censoring distribution. Results revealed that BIC tended to select underfitted models more often than the KIC and KICc. The AIC and AICc, on the other hand, tend to select overfitted models more often than the KIC and KICc. When the sample size is moderate, the AIC and AICc perform best regardless of the censoring percent. Furthermore, when the sample size is large, the KIC and KICc perform best.

Name: Diogene Pongui

Topic: Parameter identification problem to find the cardiac potential wave form in ionic models.

Abstract: In this work, we have defined an optimization problem allowing to directly find the shape of the cardiac wave of some ionic models. This allowed us to compare some of these ionic models via a parameter identification problem instead of comparing them directly by plotting the graphs for given values of the parameters. Compared to the empirical methods used to adjust one or two parameters at a time encountered in electrophysiology, we believe that our parameter identification approach is reliable and able to simultaneously identify four to eleven parameters of an ionic model. Using this approach, we adjusted the parameters of the Mitchell-Schaeffer and Aliev-Panfilov models to recover the shape of the action potential obtained experimentally by fluorescence

Keysword: Ionic models, optimal control, Nelder-Mead algorithm, parameter.

Name: Amadou Cham

Title: Stochastic Modelling of energy generation using the bivariate ARMA Models and PCA techniques for NAWEC Power Plants in The Gambia

Abstract: Energy generation and fuel consumption are the two most crucial variables in figuring out how to balance the supply and demand of electricity, particularly in urban areas with high energy demand. In order to determine the relationship between Energy Generation and Fuel consumptions as variables, the popular Box-Jenkins method and Neural Network-Principal Component Analysis (PCA) methods are employed. The purpose of the study is to model, improve and optimize the operation of NAWEC power plants in The Gambia by using bivariate ARMA models to analyze daily monitoring data on fuel consumption and energy generation. This study reconstructs Stochastic bivariate models by introducing Neural Network-Principal Component Analysis (NN-PCA) method, explores the machine learning approaches of determining Principal Components (PCs) and extracts for PCs that have major influence on data variance. The Energy Generation and Fuel Consumption Models

Y= 0.9688BK3ENG1EG + 0.2092BKENG1FC with determination factor (R-square) being 93%.

Name: Mitonsou Tierry HOUNKONNOU

Title: Differential Equation and its Applications to Covid 19

Abstract: This presentation focuses on the application of the Verhulst logistic equation, formulated by Pierre François Verhulst in 1838, to model in retrospective the total COVID-19 cases in Senegal during the period from April 2022 to April 2023. Given the ongoing COVID-19 pandemic and the need for further investigation, we utilize the solution of the Verhulst logistic equation to gain insights into the progression of the disease. Our predictions for April 2023 are compared with the actual COVID-19 data for April 2023 to assess the accuracy of the model. The data analysis is conducted using Python programming language, which allows for efficient data processing and prediction generation. By employing the solution of the Verhulst logistic equation, this research enhances our comprehension of the dynamics of COVID-19 and provides valuable insights for planning and decision-making in managing the pandemic.

Name: Michael A. Pobbi

Title: Mathematical Modelling and Analysis of Stochastic Malaria and COVID-19 Co-infection

Abstract: Due to recent climate change and disease evolution, there is the need to understand the dynamics of co-infection models. Particularly in tropical countries the presence of endemic diseases such as malaria makes diagnosis and treatment of a double burden of diseases. We present the global positive bounded solution and the basic reproduction number for the model. We study the disease-free and endemic equilibrium points stable with the suitable Lyapunov function under a certain condition. Moreover, we provide sufficient conditions for the stability of the model around the disease free and endemic equilibrium points. Finally, using a few simulation studies we demonstrate our theoretical results. We focus attention on deriving threshold values for stochastic Malaria only, stochastic COVID-19 only, and full model at disease free Rs0M, Rs0C, Rs0MC and at endemic equilibrium RsEM, RsEC, RsEMC respectively using the next generation matrix method. Next the conditions for stability for in the stochastic sense for Malaria only, COVID-19 only sub models, and full model are established. Further, we devote with full strength our concentrated attention to sufficient conditions for extinction and persistence using each of these reproductive numbers. Finally, we graphically demonstrate dynamics of co-infection by means of numerical simulations using MATLAB.

Keywords: COVID-19, Malaria, Stochastic model, Gaussian distribution, Global Stability, Local Stability

Day 4

Name: Olivier Menoukeu Pamen

Title: Takagi type curves and existence of their local time

Abstract: In this talk, we investigate Takagi-type functions with roughness parameter that are Holder continuous with coefficient. Analytical access is provided by an embedding into a dynamical system related to the baker transform where the graphs of the functions are identified as their global attractors. They possess stable manifolds hosting Sinai-Bowen-Ruelle (SBR) measures. Using moments of iterated integrals in Rademacher calculus, we prove that for some parameter a version of the Takagi-type curve centered around fibers of the associated stable manifold possesses a square integrable local time.

Name: Dorcas Attuabea Addo

Topic: End-to-.End HHL Algorithm: Pseudocode for Solving System of Linear Equation Problems (SLEP)

Abstract: The goal of research into quantum computing is to build a super computer that is powerful enough to surpass classical computers at useful computational tasks where classical computers are limited. We design an end-to-end a quantum algorithm (HHL algorithm), that solves a system of linear equation problem (SLEP). We present a pseudo-code for HHL algorithm fitting into the current use of quantum computers, bridging the start with the design for a quantum algorithm and ends with executable instructions for quantum hardware.

Name: Evans Boadi

Topic: Nonlinear water waves, solitions, integrable systems, mathematical physics, numerical solutions of PDEs

Abstract: We modified the standard AKNS method for generating integrable evolution systems to obtain new integrable peakon equations. The simplest case involving sl(2, R) matrices are considered which yield a 2−component integrable multi-peakon equations. A reduction of these equations are shown to yield 1−component peakon equations generalizing the classical Camassa-Holm equation and the modified Camassa-Holm equation. New generalized integrable peakon equations are obtained together with their Lax pair by the reduction.